Determine the effects of torsional loads on shafts.

We’re going to continue our series of articles on the calculations used in civil and mechanical engineering by diving into torsional loads on shafts and their effects. 

The image below shows a motor supplied with power which causes a shaft to rotate.  The rotating shaft causes the pulley to rotate and left a load, which gains energy.  The power input to the motor has been transmitted to the load by the shaft.  But how does this work?

If a strip of rubber is held with an end in each hand and twisted, a twisting action is seen, which transmits along the rubber.  The twisting action starts at one end of the rubber and is transmitted along it to the other hand.  The power is transmitted along the rubber by the twisting.

The shaft of the motor behaves in the same way.  The motor exerts a twisting action on one end of the shaft, and this is transmitted along the shaft, resulting in the twisting action being communicated to the pulley wheel.  This twisting action is called torsion.

The diagram below shows a shaft held rigidly at one end.  No torque is applied to the shaft on the left, and the bar is a straight line, parallel to the axis of the bar.

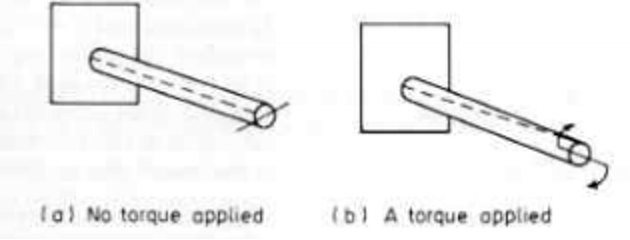
However, when a torque is applied, as we can see on the right-hand side of the diagram, the bar twists and becomes distorted.  The further down the bar from the end where the torque is applied, the less movement of the mark from its initial position. The twisting action has been transmitted down the bar, and torque has been experienced by different sections of the bar.

Torsional Stresses

Torsional stresses develop in shafts when a torsional load is applied.  Typical applications of torsional loads and stresses can be found in many aspects of engineering, wherever we find shafts to transmit power.  Some of these examples are:

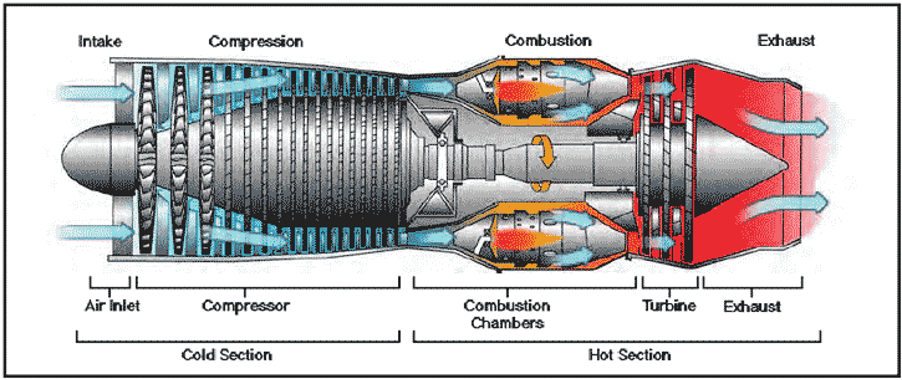
• Gas (air) enters on the left and is compressed (pressure increases) in the compressor. 
• The gas then enters the combustion chamber, where its energy is increased due to the addition of fuel and the combustion process. 
• The gas then flows through the turbine, where some energy is extracted from the now high energy flow field, and this turbine is connected to the compressor via a shaft running through the centre of the engine. 
• The remainder of the gas exits via the nozzle. 

The shaft is therefore subject to high torsional loads and stresses.

Another example can be seen below in this diagram of a marine propellor shaft:

The Calculations

Let’s check out an example:

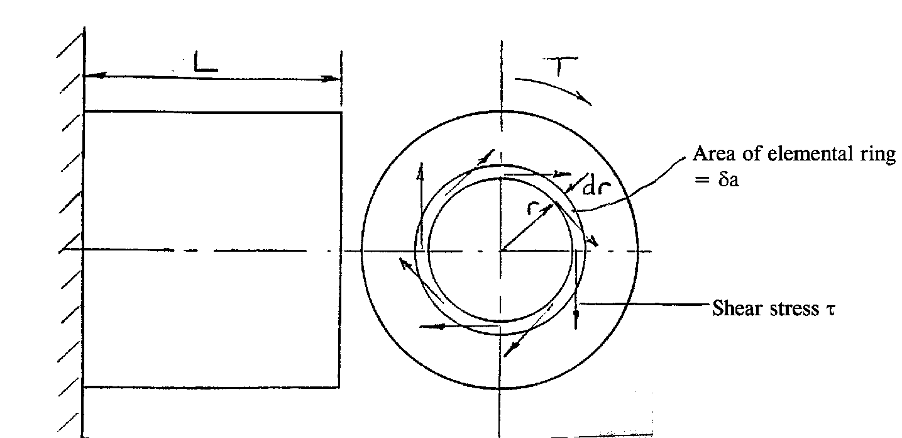
By considering the shear strain produced by twisting the shaft it can be shown that  

By considering the torque T (twisting moment) acting on the shaft is can be shown that   

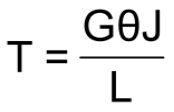
By combining these two equations we can state the following:

T = Torque

 J = Polar second moment of area

  = Shear stress at radius r

 G = Modulus of Rigidity (Shear Modulus)

  = Angle of twist over length L

For a solid shaft, with a radius of R (and diameter D):

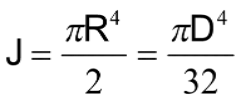
For a hollow shaft, with a radius of R (and diameter D):

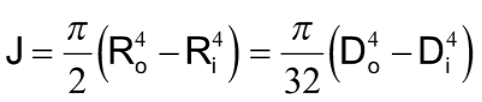
For a thin tube, t<<R, where t = thickness:

It is also useful to know the following relationship between the power of a shaft, P and the torque, T:

P=Tω

where  is the angular velocity (rad/s).

It’s worth noting that angular velocity is commonly quoted in RPM (revolutions per minute) or Hertz or Hz. (revolutions per second). However, you should note that the SI units of angular velocity are radians per second (rad/s).

Let us look at how to convert between these units. RPM60=revolutions per second=1 Hz

ω=2πf Where f = angular velocity in Hz.

Therefore: RPM60x2π=rad/s

Keep an eye out for more articles on more exciting calculations that will help you throughout your career.

Interested in our courses?

Interested in civil or mechanical engineering? Find out more about all the civil engineering courses we have available by clicking here, and the mechanical engineering courses by clicking here.

Diploma in Civil Engineering

Diploma in Mechanical Engineering

Diploma in Mechanical Technology

Diploma in Renewable Energy

Diploma in Material Science

Diploma in Sustainable Construction

Diploma in Structural Engineering

Diploma in Thermodynamics

Diploma in Building and Construction Engineering

Diploma in Thermofluids

Higher International Certificate in Civil Engineering

Higher International Diploma in Civil Engineering 

Higher International Diploma in Mechanical Engineering

Higher International Certificate in Mechanical Engineering

Alternatively, you can view all our online engineering courses here.