Introduction to Shear Force and Shear Stress

Shear force and shear stress are critical concepts in mechanics and materials science, often encountered in structural engineering and manufacturing.

• Shear Force refers to the internal force in a material that acts parallel to its cross-section. It is measured in Newtons (N). Shear force arises when two opposing forces are applied tangentially, causing the material to experience sliding or deformation along a plane.
• Shear Stress is the intensity of this force per unit area, measured in units of Pascals (Pa) or N/m². It is mathematically expressed as:

\( \tau = \frac{F}{A} \)

where:

• \( \tau \): Shear stress (Pa or N/m²)
• \( F \): Shear force (N)
• \( A \): Cross-sectional area (m²)

Everyday Examples of Shear Force and Shear Stress

Here are some practical examples where shear force and stress play a significant role:

1. Rivets and Bolts: When mechanical joints like rivets or bolts hold two plates together, they experience shear stress as forces attempt to slide the plates relative to each other.
2. Scissors: The action of cutting with scissors generates shear forces as the blades move past each other, slicing the material in between.
3. Steel Beams: In construction, beams supporting floors or bridges often experience shear forces as they bear the weight of the structure and external loads.
4. Earthquakes: Shear forces occur in tectonic plates during earthquakes, where large-scale sliding along fault lines generates stress within the Earth’s crust.
5. Sliding Doors and Windows: The rails or mechanisms that allow sliding motion are designed to withstand shear forces without deformation.

Importance of Shear Stress

Understanding shear stress is crucial for designing safe and efficient structures, machines, and tools. Engineers must ensure that materials can withstand these stresses without failure, as excessive shear can lead to cracking, slipping, or even catastrophic structural failure.

This fundamental concept has applications ranging from designing aircraft fuselages to ensuring the durability of everyday objects like nuts, bolts, and beams.

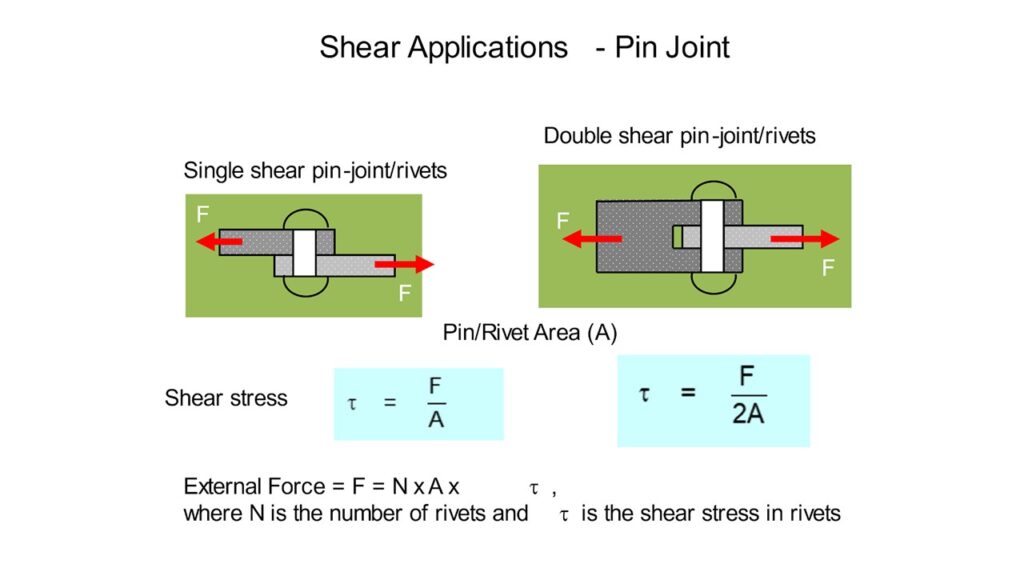
Worked Example 1: Shear Stress in a Beam

Problem Statement:

A rectangular steel beam is subjected to a shear force of \( F = 12,000 \, \text{N} \).
The cross-section of the beam has a width of \( b = 150 \, \text{mm} \) and a height of \( h = 300 \, \text{mm} \).
Assuming uniform shear stress across the cross-section, calculate the shear stress in the beam.
Also, confirm if the shear stress is within the allowable limit of \( 50 \, \text{MPa} \).

Step 1: Write Down Given Data

• Shear force: \( F = 12,000 \, \text{N} \)
• Width of the beam: \( b = 150 \, \text{mm} = 0.15 \, \text{m} \)
• Height of the beam: \( h = 300 \, \text{mm} = 0.3 \, \text{m} \)
• Allowable shear stress: \( \tau_{\text{allowable}} = 50 \, \text{MPa} = 50 \times 10^6 \, \text{N/m}^2 \)

Step 2: Formula for Shear Stress

The formula for shear stress is:

\( \tau = \frac{F}{A} \)

where:

• \( \tau \): Shear stress (\( \text{N/m}^2 \))
• \( F \): Shear force (\( \text{N} \))
• \( A \): Cross-sectional area (\( \text{m}^2 \))

Step 3: Calculate the Cross-Sectional Area

The area \( A \) of a rectangular cross-section is given by:

\( A = b \cdot h \)

Substitute \( b = 0.15 \, \text{m} \) and \( h = 0.3 \, \text{m} \):

\( A =

Worked Example 2: Single Shear Riveted Lap-Joint

Two steel plates are riveted together using ten 8 mm diameter rivets. If the shear stress in the rivet material is limited to 5 MN/m², determine the maximum shear force which the joint can support.

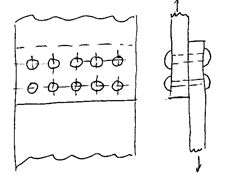
All rivets are in single shear:

Total area of 10 rivets:

\( A_{\text{total}} = 10 \cdot \frac{\pi d^2}{4} = 10 \cdot \frac{\pi (8 \times 10^{-3})^2}{4} = 502.65 \times 10^{-6} \, \text{m}^2 \)

Shear stress formula:

\( \tau = \frac{F}{A} \)

Rearranging to find the shear force:

\( F = \tau \cdot A \)

Substitute the values:

\( F = (5 \times 10^6) \cdot (502.65 \times 10^{-6}) \)

Calculate:

\( F = 2513 \, \text{N} \)

Final Answer:

The maximum shear force which the joint can support is:

\( 2513 \, \text{N} \)

Example 1: Maximum Tensile Load on a Double-Strap Butt Joint (Double Shear)

Problem Statement:
A double-strap butt joint is made with 8 rivets to join two steel plates. The diameter of each rivet is 12 mm. The maximum allowable shear stress for the rivets is 20 MN/m². Calculate the maximum tensile load that can be applied to the joint.

Step 1: Write Down Given Data

• Number of rivets: \( n = 8 \)
• Diameter of each rivet: \( d = 12 \, \text{mm} = 12 \times 10^{-3} \, \text{m} \)
• Allowable shear stress: \( \tau_{\text{max}} = 20 \, \text{MN/m}^2 = 20 \times 10^6 \, \text{N/m}^2 \)

Step 2: Formula for Shear Force on a Rivet

The shear force on a single rivet is related to its cross-sectional area and the allowable shear stress:

\( F_{\text{shear}} = \tau_{\text{max}} \cdot A \)

where:

\( A = \frac{\pi d^2}{4} \)

Step 3: Calculate the Cross-Sectional Area of One Rivet

Substitute \( d = 12 \times 10^{-3} \, \text{m} \) into the formula for \( A \):

\( A = \frac{\pi (12 \times 10^{-3})^2}{4} \)

\( A = \frac{\pi (144 \times 10^{-6})}{4} \)

\( A = 113.10 \times 10^{-6} \, \text{m}^2 \)

Step 4: Calculate Shear Force for One Rivet

Substitute \( A = 113.10 \times 10^{-6} \, \text{m}^2 \) and \( \tau_{\text{max}} = 20 \times 10^6 \, \text{N/m}^2 \):

\( F_{\text{shear}} = (20 \times 10^6) \cdot (113.10 \times 10^{-6}) \)

\( F_{\text{shear}} = 2262 \, \text{N} \)

Thus, the shear force on a single rivet is 2262 N.

Step 5: Calculate Total Shear Force for All Rivets

For \( n = 8 \) rivets:

\( F_{\text{total}} = n \cdot F_{\text{shear}} \)

\( F_{\text{total}} = 8 \cdot 2262 \)

\( F_{\text{total}} = 18096 \, \text{N} \)

Step 6: Determine Maximum Tensile Load

The maximum tensile load the joint can support is equal to the total shear force:

\( \text{Maximum Tensile Load} = F_{\text{total}} = 18096 \, \text{N} \)

Convert this to kilonewtons (kN):

\( \text{Maximum Tensile Load} = 18.1 \, \text{kN} \)

Final Answer:

The maximum tensile load that can be applied to the joint is:

\( 18.1 \, \text{kN} \)

Keep an eye out for more of our articles where we dive deeper into some of these concepts.

Interested in our engineering courses?

Interested in civil or mechanical engineering? Find out more about all the civil engineering courses we have available by clicking here, and the mechanical engineering courses by clicking here.

Diploma in Civil Engineering

Diploma in Mechanical Engineering

Diploma in Mechanical Technology

Diploma in Renewable Energy

Diploma in Material Science

Diploma in Sustainable Construction

Diploma in Structural Engineering

Diploma in Thermodynamics

Diploma in Building and Construction Engineering

Diploma in Thermofluids

Higher International Certificate in Civil Engineering

Higher International Diploma in Civil Engineering 

Higher International Diploma in Mechanical Engineering

Higher International Certificate in Mechanical Engineering

Alternatively, you can view all our online engineering courses here.