What Is The Work-Energy Theorem?

The Work-Energy Theorem is a fundamental principle in classical mechanics that connects the concepts of work and kinetic energy. It provides a powerful tool for analysing the motion of objects without relying solely on Newton’s laws in their force-acceleration form.

The principle of work and kinetic energy (also known as the work-energy theorem) states that the work done by the sum of all forces acting on a body equals the change in the kinetic energy of the particle.

The work done, W, by the net force on a body equals the change in the particle’s kinetic energy KE:

W = ∆KE = ½ mv_f² – ½ mv_i²

where v_i and v_f are the speeds of the particle before (initial) and after (final) the application of force, and m is the mass of the body.

Furthermore, the work done can also be stated as:

W = Fd

for a force, F moving a body through a distance d.

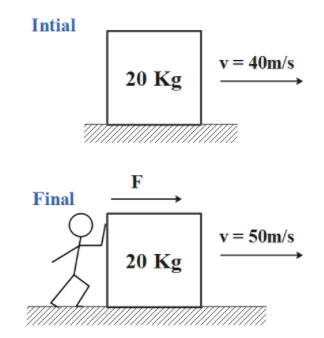
Example 1

Consider a motor car travelling at 30mph which then crashes into a stationary object such as a tree! What force is exerted on the car during this collision assuming that the vehicle compresses by 300 mm upon impact.

A typical mass of a car is around 1500kg. 

1 mile = 1609 metres

Velocity = 30mph = (30×1609) metres per hour = (30×1609)/3600 m/s = 13.4m/s

Initial kinetic energy of the car travelling at 30mph:

½ mv_f² – ½ mv_i²

KE_i = ½ mv_i² = ½ (1500)(13.4)²

KE_i = 134.8kJ

Final kinetic energy of the car is zero because it will have zero velocity.

KE_f = 0

The change in kinetic energy can be found:

∆KE = 134.8 – 0 = 134.8kJ

By the work-energy principle, the work done and the energy are related by:

W = ∆KE

Hence

W = 134.8kJ

However, recall the work done is also defined as:

W = Fd

where F is the force and d is the distance moved, which we have assumed to be the crumple zone of the car and is taken as 300 mm in this example. Therefore:

Fd = 134800

F(0.3) = 134800

F = ¹³⁴⁸⁰⁰ / _0.3

F = 450000 = 450kN

The above definition can be extended to rigid bodies by considering the work of the torque and rotational kinetic energy:

W = ∆KE _linear + ∆KE _rotational

The rotational kinetic energy of a body in angular motion, is analogous to the linear equivalent:

Now, we turn attention to the distance, x. From above, we know that:

Linear KE = ½ mv²    and Rotational KE = ½ Iω²

where m is the mass (kg) and v is the velocity (m/s), I is the moment of inertia (kgm²) and ω is the angular velocity (rad/s). Energy has SI units of Joules (J).

A body can of course also have gravitational potential energy. This is the work that has been done in raising the body to a height h above some given datum or ground level. i.e.

PE = mgh

We can now combine all of the above in to an equation for work done:

W = ∆KE _linear + ∆KE _rotational + ∆PE

The principle of conservation of energy is particularly useful when solving problems involving a combination of linear and angular motion.

A typical example is a hoist, where a load is raised by a cable on a winding drum. The driving motor must supply a torque that is sufficient to overcome the inertia of both the winding drum and the load, the weight of the load and also frictional resistance.

As x = 0 when t = 0, we can substitute this into the above equation to give:

Such a mechanical system can be represented as a ‘system’ as follows:

Where

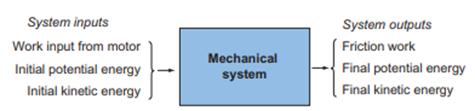
 and diagrammatically as:

An alternative way of expressing the work-energy principle is:

Total work and energy input = Total work and energy output

Work input + Initial PE + Initial KE = Final PE + Final KE + Friction work

W_i + mgh₁ + ½ mv₁² + ½ Iω₁² = mgh₂ + ½ mv₂² + ½ Iω₂² + W_f

This can be rearranged to give an equation for the input work:

W_i =  – mgh₁ – ½ mv₁² – ½ Iω₁² + mgh₂ + ½ mv₂² + ½ Iω₂² + W_f

W_i = mg (h₂-h₁) + ½ m (v₂² – v₁²) + ½I( ω₂²-ω₁²) + W_f

If the frictional resistance force F_f is known, the work done in overcoming friction can be calculated using the formula below, where s is the linear distance travelled.

W_f = F_fs

If the friction torque T_f in the bearings of a system is known, the work done in overcoming friction can be calculated using the formula below where θ is the angle turned (radians):

W_f = T_fθ

Example 2

A hoist raises a load of 75 kg from rest to a speed of 2.5 m/s whilst travelling through a distance of 6 m. The load is attached to a light cable wrapped around a winding drum of diameter 500 mm. The mass of the drum is 60 kg and its radius of gyration is 180 mm. The bearing friction torque is 5 Nm.

Determine

(a) the angle turned by the drum

(b) the final angular velocity of the drum

(c) the work input from the driving motor

(d) input torque to the winding drum

(e) the maximum power developed by the motor.

Solution:

a) The load traverses 6 m in a linear direction. This is connected to the drum and so we must relate the linear distance of 6m to the associated angular distance on the drum. 

The drum has a diameter, d, of 500 mm = 0.5 m.

The arc length, S, of a circle is defined as a section of the circle’s circumference and it is related to the angle and radius of a circle as follows:

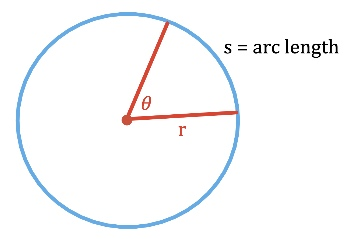
Hence:

θ = ^s / _r

In our case, the arc length will be the length of the rope that wraps around the drum which we are told is 6 m. The radius, r, is half of the drum diameter. Therefore

θ = ⁶ / _0.25

θ = 24 radians

(b)The final angular velocity

ω₂ = ^v₂ / _r

ω₂ = ^2.5 / _0.25 = 10 rad/s

c) To find the work input we must first find the moment of inertia of the drum:

I = mk²

I = (60)(0.18)²

I = 1.94 kgm²

and the work done in overcoming friction:

W_f = T_f θ

W_f = (5)(24) = 120J

Finally, the input work can be calculated given that the initial linear and angular velocities are zero (starts from rest) and the initial height can be taken as zero also:

W_i = mg (h₂-h₁) + ½ m (v₂² – v₁²) + ½I( ω₂²-ω₁²) + W_f

W_i = (75)(9.81)( 6-0) + ½ (75)(2.5² – 0²) + ½ (1.94)(10² -0²) + 120

W_i = 4414.5 + 234.375 + 97 + 120W_i = 4866.9J

(d)The input torque required to operate the drum can now be easily found:

W = Tθ

T_i = ^W_i / _θ

T_i = ^4866.8 / ₂₄

T_i = 202.8 Nm

(e)Finally, the power developed by the motor must be:

P = Tω

P_i = (202.8)(10)

P_i = 2028W or 2.03kW

Interested in our engineering courses?

We have over 70 courses across all major engineering disciplines, including, mechanical, electrical and electronic, civil, aerospace, industrial, computer and general engineering. Visit our course catalogue for a complete list of fully accredited engineering programmes.

A small selection of short courses …

Diploma in Civil Engineering

Diploma in Mechanical Engineering

Diploma in Material Science

Diploma in Structural Engineering

Level 6 Courses

International Graduate Diploma in Mechanical Engineering  

International Graduate Diploma in Civil Engineering

International Graduate Diploma in Aerospace Engineering

Level 5 Courses

Higher International Diploma in Mechanical Engineering

Higher International Diploma in Civil Engineering 

Higher International Diploma in Aerospace Engineering

Level 4 Courses

Higher International Certificate in Mechanical Engineering

Higher International Certificate in Civil Engineering 

Higher International Certificate in Aerospace Engineering

Alternatively, you can view all our online engineering courses here.

<