How do gear systems work ?

A gear is a device that can be described as a wheel with teeth located around the circumference of the wheel. A gear train is any number of gears working together to transmit rotary motion and change both the magnitude and line of action of a force, hence it can be classified as a simple machine. 

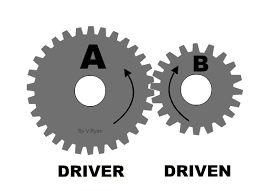
The diagram above shows a simple gear train, a combination of 2 gears, and how their teeth mesh together, our example consists of a driver and a driven gear. 

An initial effort is applied to the driver, through a shaft, for example and therefore a load is applied on the driven gear.

In such a system the teeth on the wheels are spaced so that they exactly fill the circumference with a whole number of identical teeth and the teeth on both the driver and the driven gear or ‘follower’ mesh, without interference.

From the diagram we can also see how the direction of rotation is reversed from the driver to the follower, in this instance, the driver is rotating anticlockwise, and the follower is rotating clockwise.

If the above conditions are met and the gears mesh without interference, it can be noted that the number of teeth on the driver and the follower are in direct proportion to the circumference of the gears.

^{Number of teeth on driver} / _{Number of teeth on follower}   = ^{circumference of driver} /_{circumference of follower}

This equation tells us that if there are say, 50 teeth on the driver and 25 on the follower, the circumference of the driver will be twice as big as that of the follower. 

This example can be further expanded to say that for every revolution the driver makes, the follower will make twice as many.

The gear ratio in this example is the number of teeth of the follower divided by that of the driver. So, our example gear ratio would be ²⁵/₅₀ = 0.5, often written as a gear ratio of 1:2.

Gear Ratio = ^{Number of teeth on follower} / _{Number of teeth on driver}

It then follows that the speed of rotation of the gears themselves, is inversely proportional to the number of teeth on the gear. 

For instance, as the number of teeth on the gear increases, the rotational speed of the gear decreases.

Movement ratio = ^{speed of driver} / _{speed of follower} = ^{teeth on follower} / _{teeth on driver}

Referring back to our previous example with a driver of 50 teeth and a follower of 25 teeth, the movement ratio in this case would be (²⁵/₅₀ = 0.5) A movement ratio of 0.5 indicates the driver is moving at half the speed of the follower.

Example

The diagram  shows an example gear train where the driver has 60 teeth and the follower has 15 teeth.

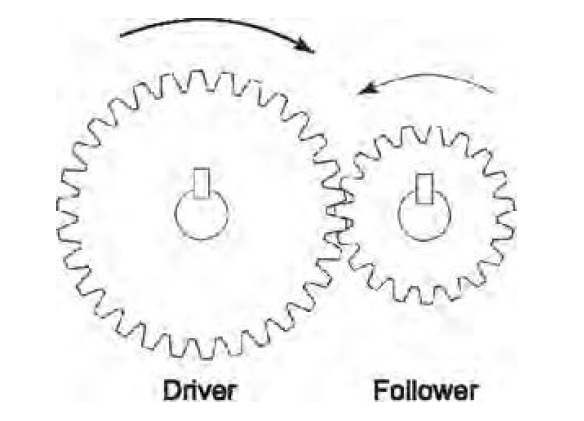
Calculate the gear ratio and movement ratio. If the driver has a  rotational speed of 200 rotations per minute, find the  speed of the follower.

To find the gear ratio,

Gear ratio = ^{Number of teeth on follower} / _{Number of teeth on driver}

Gear ratio = ¹⁵ / ₆₀ = 0.25

To find the movement ratio

Movement ratio = ^{teeth on follower} / _{teeth on driver}

Movement ratio = ¹⁵ / ₆₀ = 0.25

To find the speed of the follower:

Movement ratio = ^{speed of driver} / _{speed of follower}

Speed of follower = ^{speed of driver}  / _{Movement ratio}

Speed of follower = ²⁰⁰ / _0.25 = 800 rpm

Now considering another example, if we wished to keep the same direction of rotation for the driver and follower, we would require the addition of another gear, often referred to as an ‘idler’. 

This gear has the function of retaining the movement, or gear ratio in, the gear train but keeps the direction of the driver and follower the same.

In a more complex example, we are going to fix gears B and C to the same shaft. Hence the rotational speed of gears B and C would be the same. The gears B and C would form what is known as a compound gear train, as shown below:

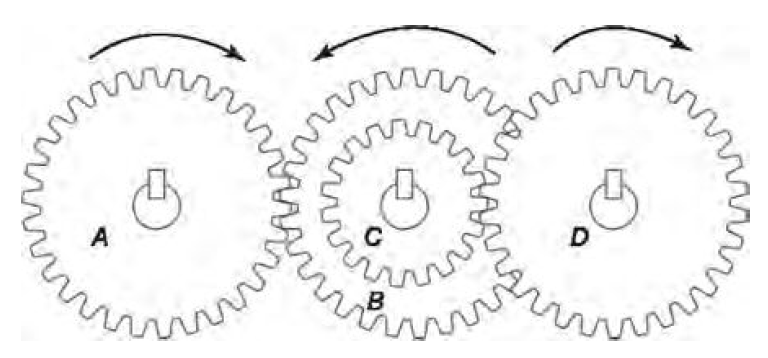
We can now derive an equation for any compound gear train to find the movement ratio of gears A and D or indeed any compound gear train having any number of gears. For the compound gear train above and using the earlier equation:

Where:

N = speed of the gear (radians per second, rad/s) or (rotations per minute, r.p.m.)

T = the number of teeth 

The equation for the movement ratio now becomes:

Movement ratio = ^N_A / _ND = ^T_B / _TA x ^T_D / _TC 

Or in general for a gear train having, say, P gear wheels, 

Movement ratio = ^N_A / _NP = ^T_B / _TA x ^T_D / _TC …..x ^T_P / _TO

Example

A compound gear train, similar to that in figure 4 consists of a driver gear, A having 60 teeth, engaging with gear B having 150 teeth. Gear C has 34 teeth and is attached to the same shaft as gear B. Gear C meshes with gear D, which has 136 teeth. The initial speed of gear A is 50 rpm. 

Calculate the movement ratio of the gear system and the speed of gear D in radians per second. 

Using equation four (with only gears A to D) 

Movement ratio = ^N_A / _ND = ^T_B / _{TA x ^TD / TC} 

Movement ratio = ^N_A / _ND = ¹⁵⁰ / ₆ x ¹³⁶ / ₃₄

Movement ratio = 2.5 x 4 = 10

The movement ratio is 10, which can also give us the speed of gear D as:

Movement ratio = ^N_A / _ND

N_D = N_A / movement ratio = ⁵⁰ / ₁₀ = 5 rpm

In order to convert this number from rotations per minute to radians per second we must multiply by 2π and divide by 60.

 ^{(5 x 2π)} / ₆₀ = 0.524 rad / s

Interested in our engineering courses?

We have over 70 courses across all major engineering disciplines, including, mechanical, electrical and electronic, civil, aerospace, industrial, computer and general engineering. Visit our course catalogue for a complete list of fully accredited engineering programmes.

A small selection of short courses …

Diploma in Civil Engineering

Diploma in Mechanical Engineering

Diploma in Material Science

Diploma in Structural Engineering

Level 6 Courses

International Graduate Diploma in Mechanical Engineering  

International Graduate Diploma in Civil Engineering

International Graduate Diploma in Aerospace Engineering

Level 5 Courses

Higher International Diploma in Mechanical Engineering

Higher International Diploma in Civil Engineering 

Higher International Diploma in Aerospace Engineering

Level 4 Courses

Higher International Certificate in Mechanical Engineering

Higher International Certificate in Civil Engineering 

Higher International Certificate in Aerospace Engineering

Alternatively, you can view all our online engineering courses here.

<