What is Friction and how can it be calculated?

Friction is a force that opposes the relative motion or attempted motion between two surfaces in contact. It plays a crucial role in our everyday lives and in engineering systems, affecting how objects start, stop, and move.

Let us consider a simple block on a surface in the figure below.

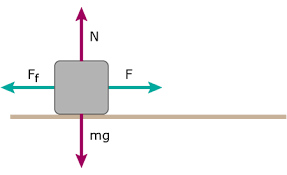
There are four forces acting on this block. 

N is the normal reaction.

mg is weight due to gravity. 

F is the sideways force applied to the block. 

F_f is the frictional force. 

The normal reaction is named as such because its direction is always normal to the surface. In this instance the normal reaction and the weight must be equal so that the block does not have resulting motion in an upwards or downwards direction. 

It is important to note that the direction of the frictional force is always opposite to the direction of motion. 

The magnitude of the frictional force depends on two factors, the size of the normal reaction and the coefficient of friction that exists between the two materials. 

The coefficient of friction is a value that increases with the amount of friction, for example a block of wood on a polished metal surface will slide relatively easily and have a low coefficient of friction and a block of wood on a rough concrete surface will not slide easily and have a higher coefficient of friction.

The equation below shows the relationship between these three variable

F_f = μ N

Where μ is the coefficient of friction (no units)

F_f is the frictional force (N)

N (sometimes denoted as R) is the normal reaction (N)

The frictional force can be described as dynamic friction, which is applicable when the block is in motion or static friction, which occurs before motion takes place. In general, the coefficient of friction for dynamic friction between two materials is less than the coefficient of static friction.

Example

A block of steel requires a force of 10.4 N applied parallel to a horizontal steel plate to keep it moving with a constant velocity across the plate. If the mass of the block is 4 kg. Determine the dynamic coefficient of friction. 

If the mass of the block is 4 kg, the weight is:

 W = mg = 4 x 9,81 = 39.2N

The weight in this instance must equal the normal reaction. R = 39.2N

F = μR

μ  = ^F/_R = ^10.4 / _39.4  = 0.265

Friction on a slope

Consider the block is now on an inclined plane. As shown below.

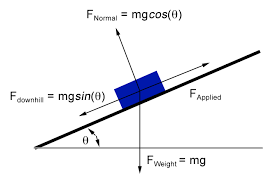
The force is now applied up the incline such that the friction opposes the motion and acts down the incline. It can also be seen that the normal reaction is acting normal to the slope and now has a value mgcosθ. There will also exist a component of weight acting down the hill, mgsinθ, that also opposes the motion and acts in the direction of friction. 

Frictional forces can be advantageous in fastening devices and keeping objects secured, they are also relied upon in braking mechanisms. However, energy is also wasted in the form of heat, generated from the friction. Physical wear and tear can occur on components causing them to not function as efficiently as designed.

Effects of friction

We will now closely examine the effects of friction on the mechanical systems we have examined so far, more specifically with regards to the screw jack. To first do this we must examine in closer detail the screw thread that is a key component of the screw jack. 

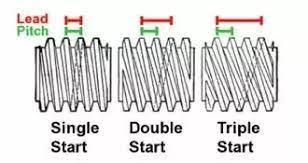
The lead is the distance moved axially by the screw in one revolution.

For a single start thread: 

lead = pitch

For a double start thread:

Lead = 2 x pitch

For a triple start thread:

Lead = 3 x pitch

Single and multi-start screw threads are used for power transmission in screw jacks, presses and machine tools. A square section screw thread can be regarded as an inclined plane which ascends in a spiralling direction. Turning the screw has the effect of moving the load up or down the incline whose angle is the helix angle, θ of the thread. 

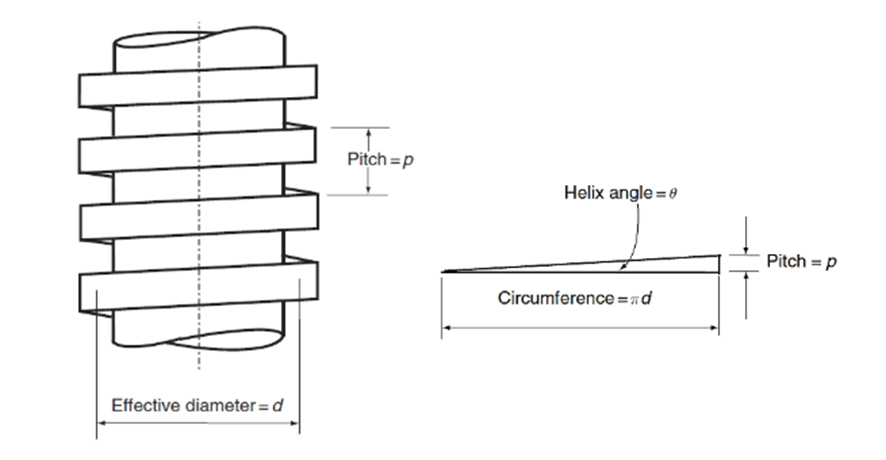
If d, is the thread diameter, the helix angle can be found from

 Tan θ = ^{lead of thread} / _{circumference of thread} = ^l / _πd

For a single-start thread, l = p and the helix angle is given by

Tan θ = ^p / _πd

There will exist an angle of friction, Φ that is directly related to the coefficient of friction, μ, by the formula:

Tan Φ = μ

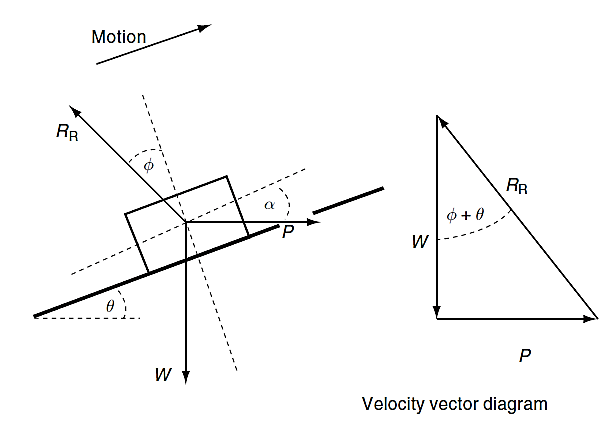
From the vector diagram above  it can be seen that the tangential force, P, required to raise the load is the same as that given by the equation below for a load raised on an inclined plane by a horizontal force. 

P = W tan (Φ + θ)

If we know the force required, we can work out the torque required to raise or lower the load, as this will just be the force multiplied by the distance (the effective radius of the thread, which is half of the effective diameter shown above.

To raise the load T = ^Wd / _{2 tan(Φ + θ)}

To lower the load T = ^Wd / _{2 tan (Φ – θ)}

The efficiency of this system can also be given by

Efficiency =  ^{tan (θ)} / _{tan (Φ + θ)}

As the angle of Friction, or as coefficient of friction itself increases, the efficiency of the system will also decrease. 

When the angle of friction, ϕ, is equal to the helix angle of the thread, θ, then tan(ϕ – θ ) = 0. 

This means the torque required to lower the load is then zero, and the screw will tend to overhaul. This is an important condition which indicates that no force is required to lower the load. The load itself will begin to turn the screw and descend down, unless a restraining torque is applied.

Example 1

A screw jack has a single start thread of pitch 8 mm and is used to raise a load of 700 kg. The required effort is 65 N, applied at the end of an operating handle 500 mm long. For these operating conditions, determine 

(a) the mechanical advantage, 

(b) the velocity ratio, 

(c) the efficiency of the machine.

Solution:

a) In this case the load is calculated from its mass. As load is a force we must multiply the mass by the acceleration due to gravity to turn the mass into the equivalent force acting downwards.

Load = 700 x 9.81 = 6867 N

M.A = ^load / _effort  = ⁶⁸⁶⁷ / ₆₅ = 106

(to 3 significant figures)

b) The velocity ratio is the distance moved by the effort divided by the distance moved by the load. In this case the distance the effort moves is a full circle with a radius of 500 mm. The distance the load moves in one pitch on the screw thread, 8 mm.

Firstly the distances must be converted to SI units, or metres in this case.

V.R = ^{distance moved by effort} / _{distance moved by load} = ^{2π x 0.5} / _0.008 = 393

c) Remembering that 

Efficiency = ^M.A / _V.R = ¹⁰⁶ / ₃₉₃ = 0.27 = 27%

Example 2

A screw jack has a square single start thread with a pitch of 15 mm and an effective diameter of 50 mm. The operating handle is 0.6 m. The coefficient of friction between the screw and operating nut is 0.3 and the load carried is 500 kg. 

Calculate:

a) the torque required to raise and lower the load,  

b) the efficiency of the jack as a lifting device and 

c) its mechanical advantage when raising this load.

The helix angle is:

Tan θ = ^p / _πd = ^0.015 / _{π x 0.05}

Tan θ = 0.0955

 θ = acrtan 0.0955 = 5.45º

The angle of friction is given by 

tan Φ =  μ

tan Φ = 0.3

Arctan 0.3 = 16.7º

We can now find the torque required to lift the load 

T = ^Wd / _{2 tan(Φ + θ)} = ^{500 x 9.81 x 0.05} / _{2 x tan (16.7 + 5.45)}

T = 49.9Nm

And the torque required to lower the load 

T = ^Wd / _{2 tan (Φ – θ)} = ^{500 x 9.81 x 0.05} / _{2 x tan ( 16.7 – 5.45)}

T = 24.4Nm

b) The efficiency is given :

Efficiency = ^{tan (θ)} / _{tan (Φ + θ)} = ^tan(5.45) / _{tan (16.7 + 5.45)} = 0.234 or 23.4%

c)

V.R = ^{distance moved by effort} / _{distance moved by load} = ^{2π x 0.6} / _0.015 = 251

Remembering the efficiency relates M.A and V.R as follows:

η  = ^M.A / _V.R

So M.A = η x V.R = 0.234 x 251 = 58.7

Interested in our engineering courses?

We have over 70 courses across all major engineering disciplines, including, mechanical, electrical and electronic, civil, aerospace, industrial, computer and general engineering. Visit our course catalogue for a complete list of fully accredited engineering programmes.

A small selection of short courses …

Diploma in Civil Engineering

Diploma in Mechanical Engineering

Diploma in Material Science

Diploma in Structural Engineering

Level 6 Courses

International Graduate Diploma in Mechanical Engineering  

International Graduate Diploma in Civil Engineering

International Graduate Diploma in Aerospace Engineering

Level 5 Courses

Higher International Diploma in Mechanical Engineering

Higher International Diploma in Civil Engineering 

Higher International Diploma in Aerospace Engineering

Level 4 Courses

Higher International Certificate in Mechanical Engineering

Higher International Certificate in Civil Engineering 

Higher International Certificate in Aerospace Engineering

Alternatively, you can view all our online engineering courses here.

<