Homepage > How can we apply the principles of energy and power to practical problems?

How can we apply the principles of energy and power to practical problems?

In our last articles, we looked at things like some of the forces that can affect engineering problems, and how we can solve problems involving distance and velocity. Now we’re going to look at how we can solve problems using the principles of energy and power.

The principle of energy

Energy is the capacity to do work. It’s a scalar quantity measured in joules. There are several different forms of energy, and energy can be transferred between the different forms. These forms are:

Kinetic: energy associated with the motion of an object with mass.
Gravitational potential: energy stored by an object at a point in a gravitational field
Elastic potential: energy stored as a result of a reversible change in an object’s shape.
Electric potential: energy of charges due to their position in an electric field.
Sound: energy of a mechanical wave due to the movement of atoms.
Internal: the sum of the randomly distributed kinetic and potential energies of the molecules in a substance.
Electromagnetic: energy from electromagnetic waves, stored within oscillating fields.
Nuclear: energy stored in nuclei, released when particles in nuclei rearrange
Chemical: energy contained in chemical bonds, released when atoms rearrange.

Although we can transfer energy between different forms, the total energy before and after the transfer is always equal. The principle of conservation of energy states that energy cannot be created or destroyed but can only be transferred from one form to another.

Power and efficiency

Power, P, is a measure of the rate at which energy is transferred. Power is the rate of work done, and its formula is

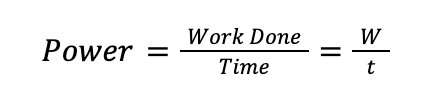
, How can we apply the principles of energy and power to practical problems?

Power is measured in watts, where one watt is defined as a rate of energy transfer of 1 joule per second. We can use the equation for power to derive an equation for the power required to move an object at a constant velocity against resistive forces (e.g. driving a car). For a car to move at a constant velocity, the net acceleration must be 0. This means the net force acting on the object must be 0, and so the magnitude of the driving force of the car, acting forward, must be equal to the resistive forces acting to oppose the motion. It is the driving force of the car that is used when considering the power required by a car to maintain a constant velocity.

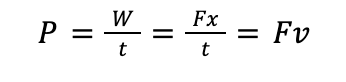
Say we have a motor and its output power is 8 kW. We can use this equation to see how much work it does in 30 seconds:

Power = work done / time taken from which, work done = power × time = 8000W × 30s = 240000J = 24 kJ.

Efficiency of a mechanical system

The conservation of energy principle states that energy is constant in a closed loop. In reality, we have energy ‘loss’, where energy is transferred from the closed loop to a form that is not as useful, such as the thermal energy generated by a lightbulb. The total energy, however, is still conserved. Efficiency is a measure of how much energy is conserved as useful energy. Greater efficiency means less energy is wasted.

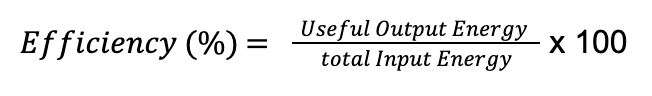
Let’s look at an example. Say a machine exerts a force of 500 N to lift a mass to a height of 7 m. If 5kJ of energy are supplied to it, what is the efficiency of the machine?

Work done in lifting mass = force × distance moved, where the force = the weight of the body. So, work done = weight × distance moved = 500N × 7m = 3500J = useful energy output

Energy input = 5 kJ = 5000J

Efficiency, η = useful output energy / input energy = 3500 / 5000 = 0.7 or 70%

4 kJ of energy is supplied to a machine used for lifting a mass. The force required is 800 N. If the machine has an efficiency of 50%, to what height will it lift the mass?

Efficiency, η = useful output energy / input energy, i.e., 0.5 = output energy /4000 J, from which, output energy = 0.5 × 4000 = 2000 J.

Work done = force × distance moved, hence; 2000J = 800N × height, from which, height = 2000J / 800N = 2.5 m